What is a Triplet Sum in an Array?

Arrays need no introduction. As a programmer, you may work with arrays almost every day. This linear data structure is extensively used in real life as well. This significant usage makes arrays an important topic to prepare for an interview or competitive exams. So, What is a Triplet Sum in an Array and how to find triplet sum?

But do you think you’ll be asked direct questions?

There is no direct answer to this question and hence, it is always better to practice than regret later.

Therefore, we have come up with a common question related to an array i.e, how to find triplet sum in array.

We are going to impart all the vital information regarding the triplet sum problem with this blog.

Understanding Problem Statement for Finding Triplet Sum in an Array

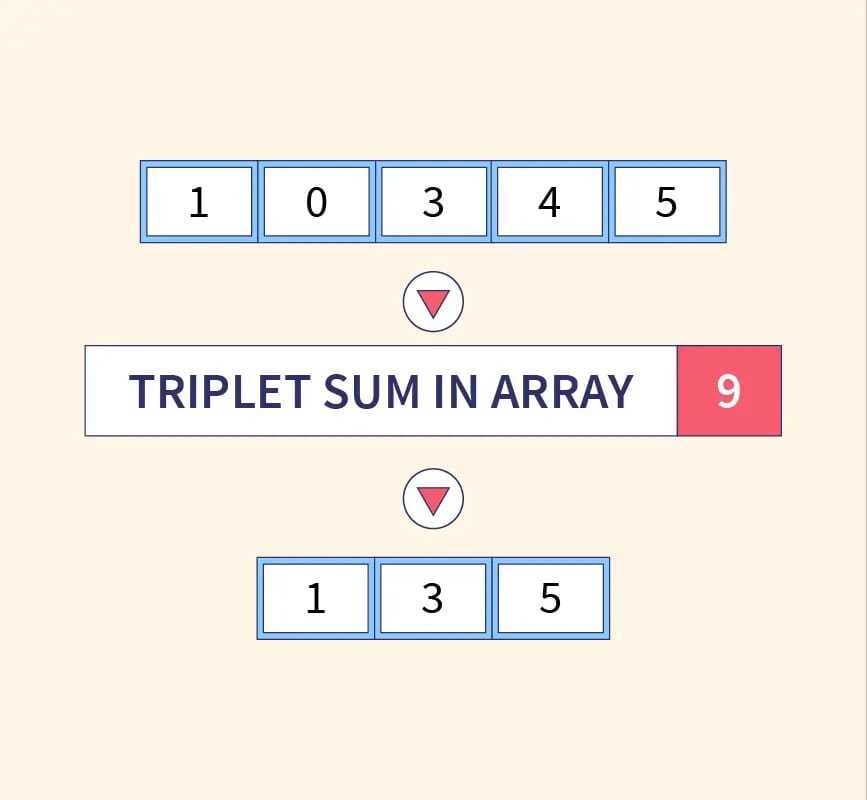
You will be provided with an array and you need to find a triplet in the array whose sum is equal to the target value.

For instance,

Given array: {1, 2, 3, 4} given sum: 6

The output will be { 1, 2, 3}

Approaches To Find Triplet Sum In An Array

The possible approaches to find triplet sum in an array includ3.e:

• Naive approach
• Recursion approach
• Hashing-based approach
• Two-Pointer approach

Naive Approach

The very basic approach to find triplet sum in array is the naive approach. The simple logic behind this approach is to find all the possible triplets present in an array and then compare the sum of each triplet to the given value.

To do this, you will have to use three nested loops.

Steps to Follow:

• You will be given a sum value and an array of size n.
• You need to now declare three nested loops. Here, the first loop will run from i to array[0]. The value of i varies from 0 to N.
• After this, the second loop will run the counter j which ranges between array[1] to n.
• Now, the last loop will run the counter k which will begin from array[2] to n.
• You will now have to calculate the sum of j, i and k. In case this sum matches the given value, you will have to print the values.
• In case no triplet has the same sum value, you need to return false.

Complexity Analysis

• Time Complexity: The time complexity of this method is calculated as O(n^3).
• Space Complexity: The space complexity of this method is calculated as O(1) because we are not using any additional space.

Recursion Method

The next method you can use to find triplet sum in an array is the recursion method. In this method, you will have to either consider the present number or leave that number.

Then you need to repeat the same process for all the other numbers present in an array. In case we exclude or include the present number and you will get the given value, you need to return.

Steps To Follow:

• To begin with, you will have to create a recursive function to determine if the required triplet exists in the array or not.
• This function will accept an array, its length, required sum and the present count.
• Now, we have to determine if the current triplet has achieved the given sum or not. In case it has the desired sum, you need to return true.
• Else, you need to return false in case the value of sum is negative.
• In the end, you need to return the recursion function with conditions.

Complexity Analysis to Find Triplet Sum in an Array

• Time Complexity: The time complexity of this method is O(3^n).
• Space Complexity: The space complexity of this method is calculated as O(N).

Hashing-Based Approach

In this method, we will be using HashSet to find triplet sum in an array. To begin with, you will have to run an inner loop from i+1 to the n positions. At the same time, you need to run the outer loop from the beginning to the end of the array.

Now, declare a HashSet to store all the elements from i+1 to j-1. You are now required to check if there is a number present in the set which is equal to target- array[i]- array[j] in case the provided total is the target value.

Steps to follow:

• From the beginning to end, you need to check all the elements of the given array with the help of counter i.
• Now, declare a HashSet and save distinct pairs in it.
• You will then have to run the loop from i+1 till n.
• if there is a number present in the set which is equal to target- array[i]- array[j], you need to print the triplet and end the loop.
• You need to then add the element present at jth location in the HashSet.

Complexity Analysis

• Time Complexity: In this method, the time complexity is calculated as O(n^2).
• Space Complexity: The space complexity is calculated as O(n).

Two-Pointers Approach

In the two-pointer approach, you need to first traverse the given array and then fix the beginning element of the triplet. You are then required to determine a pair which has a sum equal to target-array[i].

Steps to Follow:

• Begin the algorithm with sorting the given array to find triplet sum in an array.
• After this, you need to fix the beginning number of the triplet after iterating the given array.
• You will then have to use two pointers. One. At i+1 and other at i-1. Now simply find the sum.
• In case the sum is smaller than the target value, you need to increase the value of the first pointer.
• Otherwise, you need to decrease the end pointer in case the sum achieved is higher.
• Lastly, if you have found the exact value, you are required to print that triplet and break the loop.

Complexity Analysis

• Time Complexity: In this method, the time complexity is calculated as O(n^2).
• Space Complexity: The space complexity is calculated as O(1).

Conclusion: Finding Triplet Sum in an Array

Finding triplet sum in array is one of the complex and advanced level questions that you may encounter in an interview. Similarly, the sum tree problem is another one of the most-asked questions in the coding interviews.

Here, we have discussed all the four methods that you can use to find triplet sum in an array. You can choose the method that you find most optimal.

Tags: finding triplet sum in an array triplet sum in array programming what is triplet sum