Unlocking the Power of Adjusted R2 / Adjusted R-Squared: Statistics Guide

Gain a comprehensive understanding of Adjusted R2 / Adjusted R-Squared, its use cases, and its importance in statistical modeling. Whether you’re a student, researcher, or professional, this guide will help you unlock the true power of Adjusted R2.

Introduction

Statistical analysis can sometimes feel like deciphering ancient runes—mysterious, complicated, and a little intimidating. But fear not! Among the most helpful tools you’ll come across is the Adjusted R2 or Adjusted R-Squared. This metric is incredibly versatile and serves as a cornerstone in various analytical settings. In this comprehensive guide, we’ll walk you through its definition, importance, calculation, and application.

The Basics of Adjusted R2

What is it?

The Adjusted R2 is a modified version of the R-squared metric used in statistical modeling. While R-squared gives you an idea of how well your model explains the variability in your data, the Adjusted R2 fine-tunes this by penalizing the model for any unnecessary complexity. In simpler terms, it keeps your model from becoming a “Jack of all trades but master of none.”

How it Differs from R2

Imagine you’re shooting arrows at a target. The more arrows you have, the higher the chance of hitting the bullseye. But what if you have too many arrows and you can’t even draw the bowstring back? R2 is like those arrows; the more variables you add to your model, the better it will fit the data. However, R2 doesn’t care if those variables are actually useful. Enter Adjusted R2. It “adjusts” for the number of predictors in your model, helping you determine how many arrows you really need to hit that bullseye.

Importance of Adjusted R2 in Statistics

In Academic Research

Whether you’re looking to publish a groundbreaking paper or simply navigate through your post-grad thesis, Adjusted R2 can serve as your trusty companion. It helps researchers ascertain the usefulness of their models, thereby lending credibility to their findings. For example, social scientists often use Adjusted R2 to determine how factors like education level, income, and age affect voting patterns.

In Business Decision-making

In the corporate world, time is money and data is gold. Business analysts and decision-makers rely on Adjusted R2 to make informed decisions. Whether evaluating the success of a marketing campaign or forecasting sales, this metric helps ensure that only significant variables are considered, thus improving the efficiency and reliability of models.

In Machine Learning

Data scientists are the modern-day alchemists, turning data into gold (or at least actionable insights). For machine learning models, especially in supervised learning scenarios, Adjusted R2 serves as a performance metric. It helps in model selection and prevents the curse of overfitting, where the model performs exceedingly well on training data but fails on new, unseen data.

How to Calculate Adjusted R2

The Mathematical Formula

The mathematical formula for calculating Adjusted R2 is as follows:

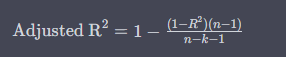
Here, $n$ is the sample size and $k$ is the number of predictors. This formula compensates for the addition of predictors, ensuring your model is just complex enough to fit the data well but not so complex that it becomes impractical.

Step-by-step Guide

Calculating Adjusted R2 can seem daunting, but it’s actually a straightforward process. Follow these steps:

1. Calculate the R2 of your model using ordinary least squares regression.
2. Determine the number of predictors ($k$) and the sample size ($n$).
3. Plug these values into the Adjusted R2 formula.

Common Tools for Calculation

You don’t have to be a math wizard to calculate Adjusted R2. Various statistical software packages such as R, Python’s Statsmodels, and SPSS can do the heavy lifting for you. Even Excel offers some rudimentary tools for this purpose.

Applications of Adjusted R2

In Regression Analysis

Regression analysis is the bread and butter of statistical modeling, and Adjusted R2 is the jam on top. It’s commonly used to evaluate the explanatory power of multiple regression models. By helping to identify the most critical variables, Adjusted R2 ensures that your model is both robust and practical.

In Economics

Economists often find themselves drowning in a sea of variables, from inflation rates to employment figures. Adjusted R2 serves as a lifeboat, helping to identify the variables that truly impact an economic model. For example, it can be used to understand how consumer spending changes in response to interest rate shifts.

In Healthcare

Adjusted R2 isn’t just for number crunchers; it also has life-saving applications. In healthcare, it’s used to model the relationship between various factors and health outcomes. For instance, epidemiologists might use Adjusted R2 to gauge the impact of lifestyle choices on heart disease risks.

In Climate Studies

Mother Nature is as complex as it gets, but Adjusted R2 helps us make sense of her ways. In climate studies, it aids in assessing how variables like carbon dioxide levels and deforestation affect global temperatures.

Limitations of Using Adjusted R2

In Non-linear Models

While R2 shines in linear models, its luster dims when it comes to non-linear ones. The reason is simple: Adjusted R2 was designed with linear relationships in mind. Thus, using it to evaluate non-linear models can give misleading results.

The Challenge of Overfitting

Even though Adjusted R2 is more resilient against overfitting compared to R2, it’s not foolproof. Sometimes a high Adjusted R2 value can give you a false sense of security, making you think your model is better than it actually is.

False Sense of Confidence

A high Adjusted R2 value might make you think you’ve cracked the code. Beware! It’s essential to remember that correlation does not imply causation. Always use Adjusted R2 in conjunction with other statistical measures and real-world logic.

How to Interpret Adjusted R2 Results

Understanding the Value Range

Adjusted R2 values range from 0 to 1, with higher values indicating a better model fit. However, unlike R2, Adjusted R2 can be negative, although this is rare and usually indicates a poorly specified model.

What High and Low Values Indicate

High values of Adjusted R2 suggest that your model explains a lot of the variability in the data. On the other hand, low values indicate that your model might be missing some key factors or is too complex for its own good.

Is Adjusted R2 Always Necessary?

While Adjusted R2 is a useful metric, it’s not always the be-all and end-all. Depending on your specific analysis, other goodness-of-fit measures like AIC or BIC might be more appropriate.

Comparison with Other Goodness-of-fit Measures

AIC and BIC

Akaike’s Information Criterion (AIC) and Bayesian Information Criterion (BIC) are other popular goodness-of-fit measures. They take into account both the model’s complexity and its ability to explain the data, just like Adjusted R2.

Mallow’s Cp

Mallow’s Cp is another alternative that adjusts for model complexity. It is especially useful when comparing models with different numbers of predictors.

Bayesian Information Criterion

This is a Bayesian approach to model selection. While it also penalizes for additional predictors, it does so in a way that is consistent with Bayesian probability theory.

Practical Examples of Using Adjusted R2

Case Study: Real Estate

In real estate, multiple factors affect property prices, from location to square footage. By using R2, analysts can create more accurate models to predict property prices, thus aiding both buyers and sellers.

Case Study: Marketing Campaign Effectiveness

Imagine you’re running multiple marketing campaigns across various channels. Adjusted R2 can help you identify which campaigns are most effective in driving customer engagement and sales, allowing you to allocate resources more efficiently.

Case Study: Environmental Science

Let’s say you’re studying the impact of industrial pollution on local wildlife. Adjusted R2 can help you quantify the relationship between pollutants and species decline, enabling more targeted conservation efforts.

Adjusted R2 in Popular Statistical Software

Python’s Statsmodels Library

Python’s Statsmodels library makes it incredibly easy to calculate Adjusted R2. Just a few lines of code, and you’re set!

R’s lm Function

In R, you can use the lm function to fit a linear model and then access the Adjusted R2 value using summary(model)$adj.r.squared.

SPSS

SPSS, the statistical software widely used in academia and industry, also offers easy ways to calculate Adjusted R2, often with just a few clicks.

Conclusion

The Adjusted R2 is more than just a statistical metric; it’s a guiding light that can illuminate the path to more accurate, reliable, and interpretable models. While it’s not without its limitations, its utility in diverse fields from academic research to machine learning cannot be overstated. So, the next time you find yourself lost in a maze of data, let R2 be your North Star.

FAQs About Adjustment R2

What is Adjusted R2 used for?

Adjusted R2 is primarily used in statistical modeling to assess the goodness-of-fit of a model. It helps to evaluate how well the model explains the variability in the dependent variable, while taking into account the number of predictors used. Unlike R2, it penalizes the model for including predictors that don’t improve the model’s ability to predict. It is widely used in various fields including academic research, economics, machine learning, healthcare, and business analytics.

How does Adjusted R2 differ from R2?

Both R2 and R2 provide a measure of how well the model fits the data. However, the key difference is that R2 for the number of predictors in the model. While R2 increases as you add more predictors, regardless of their usefulness, R2 will decrease if the new variables don’t improve the model’s fit. This makes R2 a more robust metric when comparing models with different numbers of predictors.

Is a higher Adjusted R2 always better?

Generally, a higher Adjusted R2 indicates a better model fit, as it suggests that the model explains a larger portion of the variability in the data. However, a high Adjusted R2 is not a guarantee of a good model. It’s essential to consider other diagnostic tests and goodness-of-fit measures, as well as the logical and theoretical reasoning behind including specific predictors in the model.

Can Adjusted R2 be negative?

Yes, unlike R2, which is bounded between 0 and 1, R2 can be negative. However, a negative R2 is generally a sign that the model is a poor fit for the data, and it usually occurs when the model does worse than a horizontal line (mean model) in predicting the output. It’s rare but serves as a warning that the model is probably overfitted or fundamentally flawed.

What are the limitations of Adjusted R2?

1. Non-linear Models: Adjusted R2 is best suited for linear models and may produce misleading results for non-linear models.
2. Overfitting: While it’s better than R2 at avoiding overfitting, a high Adjusted R2 can still give a false sense of model quality.
3. Correlation ≠ Causation: A high Adjusted R2 doesn’t confirm that the predictors cause the dependent variable to change; it only signifies a relationship.
4. Requires Careful Interpretation: Like any statistical measure, R2 should be used in conjunction with other tests and domain-specific knowledge for robust model evaluation.