Power of Bayesian Inference in Data Science: From Concepts to Real-World Impact
In the intricate and rapidly evolving realm of Data Science, Bayesian Inference emerges as a cornerstone for robust, data-driven decision-making. Whether you’re aiming to decode intricate customer behavior, construct predictive models, or delve into the complexities of AI and machine learning, Bayesian Inference offers a potent mathematical framework. This guide delves deep into the essence of Bayesian Inference in Data Science, its historical context, and how its prowess can be harnessed across real-world applications.
Table of Contents
What is Bayesian Inference?
Deciphering Bayesian Inference: A Foundation for Informed Decisions
At its core, Bayesian Inference is a statistical technique that empowers you to recalibrate hypothesis probabilities based on fresh evidence. The technique finds its roots in conditional probability and thrives on the bedrock of Bayes’ Theorem, rendering it a robust tool for refining decisions as new data emerges.
Bayesian vs. Frequentist Statistics
Pioneering a New Path: Bayesian vs. Frequentist Approaches
Bayesian Inference stands apart from its frequentist counterpart due to its focus on probability distributions over fixed parameters. This unique approach imparts a nuanced understanding of data that aligns with real-world complexities, including uncertainties and variabilities, making it an invaluable asset for data interpretation.
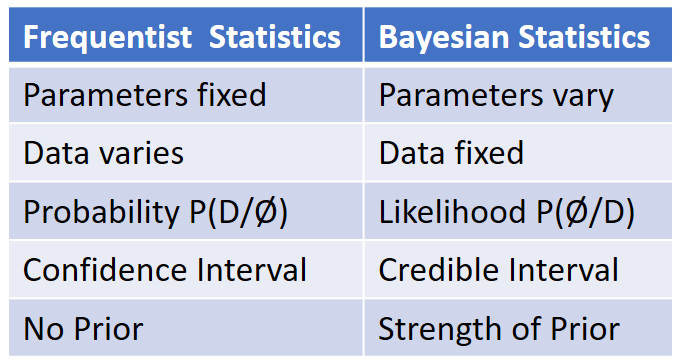
Bayesian vs. Frequentist Approaches
Historical Context of Bayesian Inference
Tracing the Origins: Unraveling the Historical Fabric of Bayesian Inference
Named after the visionary 18th-century statistician and philosopher Thomas Bayes, this technique carries a rich historical tapestry. Over the years, Bayesian Inference has evolved, adapting to modern statistical and data science demands, becoming a linchpin in machine learning, predictive analytics, and statistical modeling.
Evolution Over Time
From Modest Beginnings to Impactful Present: Bayesian Inference’s Journey
Bayesian Inference’s journey from its humble origins has transformed it into a pivotal element within academic research and industrial applications. This metamorphosis has laid the foundation for its indispensable role in areas like machine learning, predictive analytics, and statistical modeling.

Bayesian Model
Importance of Bayesian Inference in Data Science
A Versatile Arsenal: Bayesian Inference’s Realm of Applications
In a world driven by data, Bayesian Inference assumes the role of a Swiss Army knife in the data science arsenal. Its applications transcend industries, spanning healthcare, finance, machine learning algorithms, and risk management, making it a dynamic solution for dissecting intricate data landscapes.
Why Bayesian Inference is Crucial
Precision and Depth: The Essence of Bayesian Inference’s Significance
Bayesian Inference’s hallmark attributes of adaptability, precision, and depth elevate its status as a non-negotiable asset when navigating intricate data structures and crafting informed decisions rooted in data-driven insights.
5 Main Principles of Bayesian Inference in Data Science: Strategies, Examples, and Practicality
Principle #1: Bayes’ Theorem
Unveiling the Core: Bayes’ Theorem in Action
Bayes’ Theorem resides at the epicenter of Bayesian Inference, offering a mathematical framework to recalibrate probabilities based on emerging evidence. A mastery of this theorem serves as a springboard for exploring advanced Bayesian concepts, paving the way for in-depth data exploration.
Practical Application of Bayes’ Theorem in Data Science
Imagine a diagnostic scenario in healthcare. Let’s say a new medical test for a rare disease has been developed. Prior to testing, we have a belief that only 1% of the population has this disease. The test has an accuracy of 95%, meaning it correctly identifies the disease 95% of the time and gives a false positive 5% of the time.
Let A be the event that a person has the disease, and B be the event that the test is positive. We want to calculate the probability that a person actually has the disease given that the test is positive: P(A|B).
Using Bayes’ Theorem:
P(A|B) = (P(B|A) * P(A)) / P(B)
P(B|A) is the accuracy of the test, which is 0.95. P(A) is the prior probability of having the disease, which is 0.01. P(B) is the probability of the test being positive, which can be calculated as follows: P(B) = P(B|A) * P(A) + P(B|~A) * P(~A) P(B|~A) is the probability of the test being positive given that the person doesn’t have the disease, which is 0.05. P(~A) is the complement of having the disease, which is 1 – P(A).
After plugging in these values, we can calculate P(B):
P(B) = (0.95 * 0.01) + (0.05 * 0.99) = 0.0594
Finally, we can calculate P(A|B):
P(A|B) = (0.95 * 0.01) / 0.0594 ≈ 0.1602
This means that even if the test is positive, there’s still only about a 16.02% chance that the person actually has the disease. This example demonstrates how Bayesian Inference combines prior beliefs with new evidence to arrive at more accurate probabilities.
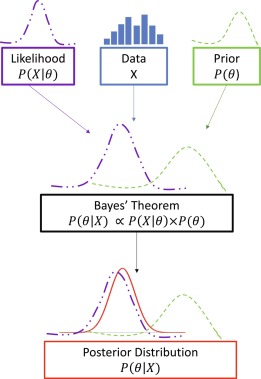
Bayesian Model
Principle #2: Prior and Posterior Distributions
Navigating Beliefs: Prior and Posterior Distributions Deciphered
Prior distributions encapsulate pre-existing beliefs before fresh data enters the fray, while posterior distributions reshape these beliefs post-new data assimilation. These twin concepts underpin the very essence of Bayesian Inference, dictating the trajectory of updated probabilities.
Real-world Applications
Whether predicting stock market fluctuations or delivering precise medical diagnoses, an adept comprehension of prior and posterior distributions stands as a bedrock for precision-driven data understanding, driving accurate decision-making.
Principle #3: Likelihood
Bridging the Gap: The Crucial Role of Likelihood
The concept of likelihood quantifies the extent to which observed data elucidates the parameter under scrutiny. Serving as a bridge between prior and posterior distributions, likelihood facilitates the seamless refinement of data insights with each iterative step.
Principle #4: Conjugate Priors
Balancing Act: Unveiling Conjugate Priors’ Pros and Cons
Conjugate priors offer a shortcut to streamline posterior distribution updates, yet their convenience doesn’t always align with an accurate data representation. Also, a comprehensive grasp of their utility empowers the artful equilibrium between mathematical simplicity and data fidelity.
Principle #5: Markov Chain Monte Carlo Methods
Navigating Complex Terrain: Markov Chain Monte Carlo Demystified
Markov Chain Monte Carlo (MCMC) methods are the unsung heroes that approximate intricate posterior distributions. Also, their significance amplifies in the realm of multi-dimensional data spaces, particularly in cases where conventional optimization techniques falter.
Practical Applications of MCMC in Data Science
Imagine a scenario where you’re designing a recommendation system for an e-commerce platform. Also, Bayesian Inference can be instrumental in personalizing recommendations based on user preferences and behavior.
Let’s say you’re trying to recommend movies to users. Each movie has multiple features like genre, director, and cast. Also, you want to find the best combination of features that align with a user’s taste.
MCMC methods can help you sample from the posterior distribution of these features given the user’s preferences and interactions. By using MCMC, you can iteratively refine the recommendations, adjusting the feature combination to better match the user’s preferences. This way, you navigate the complex feature space efficiently and provide tailored recommendations.
Bayesian Inference Tools and Software
Harnessing Efficiency: Leading Bayesian Tools
Tailored tools like Stan and PyMC3 emerge as champions in the realm of Bayesian model implementation. Also, strategic tool selection wields the potential to revolutionize the efficiency and reliability of your Bayesian endeavors.
How to Choose the Right Tool
Nurturing Selection Wisdom: Guiding the Tool Choice
Navigating the realm of Bayesian tools mandates a strategic evaluation of your unique requisites, project intricacies, and your expertise spectrum. Also, the harmonious interplay of these factors magnifies the potency of your Bayesian model’s impact.
Practical Examples of Bayesian Inference in Data Science
Healthcare Revolution: Unleashing Bayesian Potential
In healthcare, Bayesian methods propel the transformation of patient outcome predictions, personalizing treatment blueprints, and optimizing resource allocation within hospitals. Also, this revolution reshapes patient care and operational efficiency.
Empowering Financial Decisions: Bayesian Finance Applications
From assessing risks to fine-tuning portfolio optimization, Bayesian methodologies forge the bedrock for astute data-driven financial decisions. Also, this prowess resonates across risk quantification and investment strategy domains.
Pitfalls to Avoid
Navigating Pitfalls: Safeguarding Bayesian Integrity
Similar to any statistical methodology, Bayesian Inference is susceptible to misuse. Also, Pitfalls such as overfitting and underfitting can mar data-driven insights. Vigilance, rigorous model validation, and extensive cross-dataset testing serve as sentinels against these missteps.
How to Avoid These Mistakes
Crafting Vigilance: Mitigating Bayesian Errors
Cultivating cautiousness, rigorous model validation, and comprehensive testing across diverse datasets serve as the armor to shield against common Bayesian pitfalls. These practices empower you to craft accurate and impactful Bayesian models.
How to Get Started with Bayesian Inference in Data Science
Building the Foundation: Preparing Your Data
In the realm of stock market prediction, the quality of prior information is a linchpin in Bayesian models’ performance. Also, scrutinizing historical financial data, curating meaningful priors, and aligning them with economic indicators unfurl the potential for precision-driven insights.
Implementing Bayesian Models
While implementation can pose challenges, a solid understanding of Bayesian principles coupled with adept tool utilization can culminate in actionable insights and transformative predictive models. Also, this synergy has the potential to reshape business trajectories and propel groundbreaking research.
Conclusion
Empowering the Data Odyssey: Bayesian Inference’s Unparalleled Eminence
More than a statistical method, Bayesian Inference metamorphoses into a potent framework equipping you with the analytical finesse to navigate a data-rich universe. From the annals of history to the frontiers of modern applications, Bayesian Inference stands tall as an indispensable ally for every data scientist. With this comprehensive guide in hand, embark on your Bayesian journey, harness the power of data-driven enlightenment, and stride confidently into the intricate realms of data science.
Hello, I’m Cansu, a professional dedicated to creating Excel tutorials, specifically catering to the needs of B2B professionals. With a passion for data analysis and a deep understanding of Microsoft Excel, I have built a reputation for providing comprehensive and user-friendly tutorials that empower businesses to harness the full potential of this powerful software.
I have always been fascinated by the intricate world of numbers and the ability of Excel to transform raw data into meaningful insights. Throughout my career, I have honed my data manipulation, visualization, and automation skills, enabling me to streamline complex processes and drive efficiency in various industries.
As a B2B specialist, I recognize the unique challenges that professionals face when managing and analyzing large volumes of data. With this understanding, I create tutorials tailored to businesses’ specific needs, offering practical solutions to enhance productivity, improve decision-making, and optimize workflows.
My tutorials cover various topics, including advanced formulas and functions, data modeling, pivot tables, macros, and data visualization techniques. I strive to explain complex concepts in a clear and accessible manner, ensuring that even those with limited Excel experience can grasp the concepts and apply them effectively in their work.
In addition to my tutorial work, I actively engage with the Excel community through workshops, webinars, and online forums. I believe in the power of knowledge sharing and collaborative learning, and I am committed to helping professionals unlock their full potential by mastering Excel.
With a strong track record of success and a growing community of satisfied learners, I continue to expand my repertoire of Excel tutorials, keeping up with the latest advancements and features in the software. I aim to empower businesses with the skills and tools they need to thrive in today’s data-driven world.
Suppose you are a B2B professional looking to enhance your Excel skills or a business seeking to improve data management practices. In that case, I invite you to join me on this journey of exploration and mastery. Let’s unlock the true potential of Excel together!
https://www.linkedin.com/in/cansuaydinim/










