Navigating Investment Risks: Deviation Risk Measures
Introduction: Why Understanding Risk is Crucial for Investors
Whether you’re a beginner investor or a seasoned pro, understanding investment risks is as crucial as understanding returns. Enter Deviation Risk Measures, a term that, although not standardized in the finance sector, helps you quantify different forms of investment risk. From Standard Deviation to Value at Risk, this guide aims to take you from the basics to the advanced nuances of these critical metrics.
Table of Contents
Risk Measures Decoded: The Core Metrics
Standard Deviation: Your Go-To Risk Indicator
Standard Deviation is generally the first point of entry for assessing investment risk. It quantifies how much individual data points deviate from the mean or average. A higher value indicates more significant volatility and, by extension, greater risk.
The Standard Deviation Formula
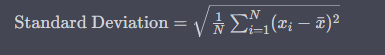
Deviation Risk Measures Formula
Value at Risk (VaR): Setting Financial Boundaries
Value at Risk (VaR) offers a quick snapshot of your potential loss within a specific timeframe at a chosen confidence level. For instance, a one-day 95% VaR of $1 million implies a 5% probability of exceeding this loss in one day.
Conditional Value at Risk (CVaR): The ‘Beyond’ Measure
Also known as Expected Shortfall, Conditional Value at Risk (CVaR) explores what you can expect to lose in worst-case scenarios—those that go beyond VaR. It’s vital for understanding tail risk.
Tracking Error: Measuring Consistency
If you’re comparing your investment against a benchmark index, Tracking Error tells you how consistently your portfolio tracks it. A lower value indicates better consistency.
How to Calculate Deviation Risk Measures: From Beginner to Pro
Calculating Standard Deviation: A Step-By-Step Guide
- Calculate the mean (�ˉ) of your set of returns.
- Subtract the mean from each return (��), then square it.
- Average these squared deviations.
- Square root of the average gives you the Standard Deviation.
Computing Value at Risk (VaR): Methods and Models
- Select your time frame and confidence level.
- Use historical data or Monte Carlo simulations to find a distribution of returns.
- Identify the worst-case loss for the chosen confidence level.
Determining Conditional Value at Risk (CVaR): Beyond VaR
- Start by calculating VaR at your chosen confidence level.
- Average out returns worse than the VaR level.
Measuring Tracking Error: Simple Yet Crucial
- Calculate returns for your portfolio and benchmark index.
- Compute the difference between these returns.
- Calculate the standard deviation of these differences.
Advanced Concepts: Deduction Methods and Inter-Relationships
From Standard Deviation to VaR: A Logical Transition
Often, Standard Deviation and VaR are used in tandem. If the returns are normally distributed, you can deduce VaR from the Standard Deviation using Z-scores—a statistical multiplier applied to the standard deviation.
VaR and CVaR: Two Sides of the Same Coin
It’s beneficial to use VaR and CVaR together, as they provide a more comprehensive risk profile. While VaR sets a boundary, CVaR gives an average of what happens beyond that boundary.
Tracking Error and Standard Deviation: A Comparative Analysis
The Tracking Error is often compared with Standard Deviation to gauge how a portfolio deviates from both its mean and its benchmark. A lower Tracking Error usually indicates lower standard deviation relative to the benchmark index.
Conclusion: Tailor Your Risk Measures for Better Investments
Choosing the Deviation Risk Measure that aligns with your investment goals and risk tolerance can significantly improve your risk assessment and investment decisions. Whether you’re a novice in the investment landscape or a seasoned investor, these metrics are invaluable tools to have in your investment toolkit.
Disclaimer: This information is for educational purposes only. Always consult a certified financial advisor before making any investment decisions.
Additional Insights: Behavioral and Regulatory Considerations
Behavioral Aspects: Investor Psychology and Risk Measures
Understanding Deviation Risk Measures is also crucial from a behavioral perspective. Investors are often subject to emotional and cognitive biases, like overconfidence or loss aversion, that can adversely affect their investment choices. Accurate risk measures can serve as reality checks, making investors more aware of the actual volatility and potential loss tied to their investments.
Regulatory Compliance: A Must-Have
In many jurisdictions, especially for hedge funds and mutual funds, there are regulatory requirements around risk disclosure. Not only do Standard Deviation, VaR, and CVaR offer valuable insights, but they are also often required for compliance with financial regulations. Understanding how to calculate and interpret these metrics is crucial for both individual and institutional investors to stay on the right side of the law.
Common Mistakes and How to Avoid Them
Relying Solely on One Measure
One common mistake investors make is to rely solely on one risk measure. No single metric can capture all the complexities and nuances of market risk. For a holistic understanding, it’s advisable to use a combination of Deviation Risk Measures.
Misunderstanding the Limitations
Another pitfall is not understanding the limitations of each measure. For example, Standard Deviation assumes a normal distribution of returns, which may not always be the case. VaR doesn’t give any insight into losses that could occur beyond the specified confidence level. Being aware of these limitations helps in using the measures more effectively.
Final Thoughts: The Path Ahead in Risk Management
As we’ve seen, understanding Deviation Risk Measures is not just about crunching numbers; it’s about making more informed decisions, complying with regulations, and even understanding investor psychology. Whether you’re a beginner or a seasoned investor, these metrics are indispensable tools that can significantly improve your investment decision-making process.
Disclaimer: The information in this blog post is intended for educational purposes and should not be considered financial advice. Always consult a certified financial advisor for personalized investment guidance.
By understanding and applying these risk measures effectively, you can navigate the financial markets with greater confidence and precision. So go ahead, add these powerful tools to your investment toolkit, and make your financial journey more rewarding and secure.
Practical Examples: Applying Deviation Risk Measures in Real Life
Understanding these concepts is vital, but how about applying them? Let’s take a real-world example to understand how these Deviation Risk Measures can be practically employed.
Example: Assessing Risk of a Stock Portfolio Using Standard Deviation, VaR, and CVaR
Context
Let’s say you have a portfolio consisting of three different stocks: Stock A, Stock B, and Stock C. Over the last year, you’ve tracked their monthly returns, and now you’re interested in assessing the risk associated with your portfolio.
Calculating Standard Deviation
- Collect Monthly Returns: Assume the average monthly return of your portfolio is 5%.
- Subtract the Mean and Square: Say, for one month, Stock A gives a return of 7%. The squared deviation would be (7.
- Average the Squared Deviations: If you do this for all returns over the past 12 months, you might get an average squared deviation of, say, 0.03.
- Calculate Standard Deviation: The square root of 0.03 is approximately 0.1732 or 17.32%.
Your portfolio has a Standard Deviation of 17.32%, indicating its risk or volatility.
Calculating Value at Risk (VaR)
- Select Time Frame and Confidence Level: Let’s choose a one-day time frame and a 95% confidence level.
- Use Historical Data: If the worst 5% of past one-day returns are a loss of 3% or more, then your one-day 95% VaR is 3%.
This means that there is a 5% chance that you could lose 3% or more in one day.
Calculating Conditional Value at Risk (CVaR)
- Start with VaR: Your one-day VaR is 3%.
- Average Out Worse Returns: If the average of returns that are worse than -3% is -4%, your one-day CVaR would be 4%.
This indicates that when things go badly (beyond the VaR), you can expect an average loss of 4%.
Interpretation
- Standard Deviation tells you that your portfolio’s returns can generally deviate by 17.32% from the mean.
- VaR tells you that there’s a 5% chance of losing 3% or more in one day.
- CVaR provides additional insight into the severity of losses when things go south, suggesting an average loss of 4% in the worst-case scenarios.
By going through this example, you can see how Deviation Risk Measures can help you quantify the risk of your investment portfolio in different ways, offering a more well-rounded view of your potential risk exposure.
Hello, I’m Cansu, a professional dedicated to creating Excel tutorials, specifically catering to the needs of B2B professionals. With a passion for data analysis and a deep understanding of Microsoft Excel, I have built a reputation for providing comprehensive and user-friendly tutorials that empower businesses to harness the full potential of this powerful software.
I have always been fascinated by the intricate world of numbers and the ability of Excel to transform raw data into meaningful insights. Throughout my career, I have honed my data manipulation, visualization, and automation skills, enabling me to streamline complex processes and drive efficiency in various industries.
As a B2B specialist, I recognize the unique challenges that professionals face when managing and analyzing large volumes of data. With this understanding, I create tutorials tailored to businesses’ specific needs, offering practical solutions to enhance productivity, improve decision-making, and optimize workflows.
My tutorials cover various topics, including advanced formulas and functions, data modeling, pivot tables, macros, and data visualization techniques. I strive to explain complex concepts in a clear and accessible manner, ensuring that even those with limited Excel experience can grasp the concepts and apply them effectively in their work.
In addition to my tutorial work, I actively engage with the Excel community through workshops, webinars, and online forums. I believe in the power of knowledge sharing and collaborative learning, and I am committed to helping professionals unlock their full potential by mastering Excel.
With a strong track record of success and a growing community of satisfied learners, I continue to expand my repertoire of Excel tutorials, keeping up with the latest advancements and features in the software. I aim to empower businesses with the skills and tools they need to thrive in today’s data-driven world.
Suppose you are a B2B professional looking to enhance your Excel skills or a business seeking to improve data management practices. In that case, I invite you to join me on this journey of exploration and mastery. Let’s unlock the true potential of Excel together!
https://www.linkedin.com/in/cansuaydinim/










