Unlocking the Secrets of Arithmetic Mean: The Ultimate 2023 Guide to Understanding This Powerful Statistical Tool
Step into the world of statistics with our comprehensive Arithmetic Mean: Statistics Guide. Discover how the arithmetic mean is more than just an average number and why it’s crucial in data analysis.
Table of Contents
Introduction
Step right in, because you’re about to embark on a fascinating journey through the world of statistics, specifically focusing on the Arithmetic Mean. Think of the arithmetic mean as the cornerstone in the edifice of statistics. Whether you’re a student grappling with your first stats class, a professional knee-deep in data, or simply a curious individual, this guide will be your north star.
What is Arithmetic Mean?
Definition
The arithmetic mean is what most of us commonly refer to as the “average.” It’s calculated by adding all the numbers in a data set and then dividing the sum by the count of those numbers.
Importance
While the concept may seem trivial, the arithmetic mean holds paramount importance in statistics. It serves as a representative figure for a data set, offering a snapshot of what the “typical” data point might look like.
Simple Examples
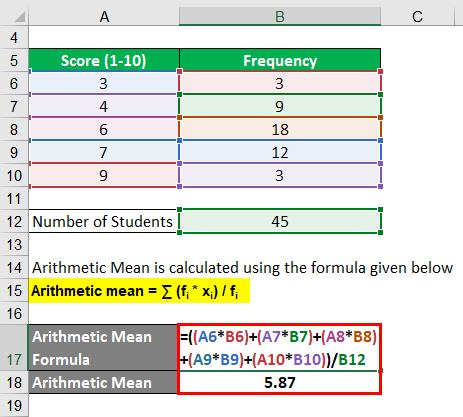
Take the scores of a basketball player over five games: 10, 15, 20, 25, and 30 points. The arithmetic mean would be (10+15+20+25+30)/5 = 20 points. This number, 20, tells us that the player’s average performance is 20 points per game.
Arithmetic Mean Vs. Other Types of Mean
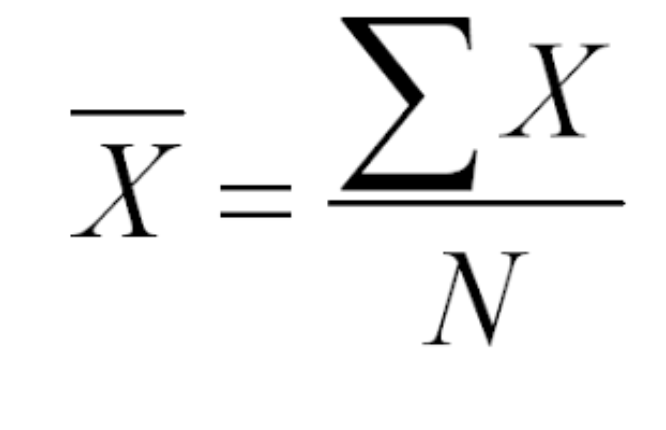
Geometric Mean
While the arithmetic mean is the average most people are familiar with, the geometric mean is another way to find a “middle ground.” The geometric mean is more appropriate for comparing different products or investments that have different bases.
Harmonic Mean
The harmonic mean is another variant, generally used when dealing with rates. For example, if you’re interested in speed, the harmonic mean provides a more accurate average than the arithmetic mean.
Calculating the Arithmetic Mean
Basic Formula
The basic formula for calculating the arithmetic mean is simple:
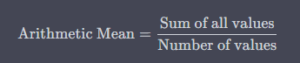
Step-by-Step Guide
- Add up all the numbers in your data set.
- Count the total number of values.
- Divide the sum by the number of values.
It’s as easy as 1-2-3!
Arithmetic Mean in Daily Life
Shopping
When grocery shopping, you can use the mean to find the average cost per unit of different products. Also, this allows you to make an informed decision on which product provides the best value.
Sports
In sports, the mean can help you evaluate a player’s average performance over a period, helping in draft selections or strategy formulation.
Education
In the educational sector, the mean is commonly used to calculate the average grades for a class or an individual student’s performance over a term.
Use Cases in Professional Fields
Finance
In finance, the mean is often used to calculate the average return on investment, helping investors make decisions.
Medicine
In medical research, the mean of patient responses, age groups, or other variables can offer invaluable insights into the effectiveness of a treatment.
Social Sciences
In fields like psychology or sociology, the mean can help researchers understand and interpret social phenomena, such as average income levels or educational attainment.
Arithmetic Mean and Population
Sampling
In statistics, a sample is often used to estimate the mean of a whole population. This is crucial in fields like polling or market research.
Population Mean
The mean of a population includes every single data point in that population and is usually represented by the Greek letter mu (μ).
Importance in Data Analysis
Variability
The mean provides a measure of central tendency, but when used in tandem with other statistical measures like variance or standard deviation, it offers a fuller picture of data variability.
Central Tendency
One of the key roles of the mean is to measure the ‘central tendency’ of a dataset, which helps to summarize a dataset with a single value that represents its ‘center.’
Arithmetic Mean in Research
Surveys
In surveys, the arithmetic mean can provide a general sense of public opinion, helping policymakers or corporations to tailor their strategies accordingly.
Experiments
In controlled experiments, the mean can summarize the outcomes, offering a singular value that represents the experiment’s effect.
Observational Studies
In observational studies, the arithmetic mean can help researchers draw inferences about larger populations based on sampled data.
Variants and Modifications
Weighted Mean
In some instances, not all data points in a set carry the same level of importance. Also, this is where the weighted mean comes into play, allowing for a more nuanced analysis.
Trimmed Mean
When outliers disproportionately affect the arithmetic mean, a trimmed mean can offer a more representative average by removing the highest and lowest values.
Common Pitfalls
Outliers
A single outlier can significantly skew the arithmetic mean, providing a misleading representation of a dataset.
Misinterpretations
The arithmetic mean is just one measure among many. Using it in isolation can sometimes lead to inaccurate interpretations or conclusions.
Arithmetic Mean and Probability
Expected Value
In probability theory, the arithmetic mean becomes the ‘expected value’ of a random variable, indicating what one can expect to happen on average.
Random Variables
The arithmetic mean serves as the foundation for the expected value in random variables, often used in simulations or modeling.
Arithmetic Mean in Excel
Functions
In Excel, the AVERAGE function can quickly calculate the arithmetic mean of a range of cells.
Manual Calculation
You can also manually calculate it by summing up the numbers with the SUM function and then dividing by the count of numbers.
How Technology is Changing Arithmetic Mean Calculations
Software
New statistical software allows for more complex mean calculations, such as weighted means or multi-variable analysis.
Big Data
With the advent of big data, the mean can now be calculated for extremely large datasets, providing more accurate and robust results.
Arithmetic Mean in Python
Libraries
Python libraries like NumPy and pandas offer built-in functions to easily compute the mean.
Code Examples
Python makes it extremely straightforward to calculate the mean. Here’s a simple code snippet using NumPy:
import numpy as np
data = [1, 2, 3, 4, 5]
mean = np.mean(data)
How to Interpret Arithmetic Mean
Context
Like any statistic, the arithmetic mean needs to be interpreted in the context of the data it represents.
Comparative Analysis
Comparing arithmetic means from different datasets or periods can provide valuable insights into trends or differences.
Limitations of Arithmetic Mean
When Not to Use
Despite its usefulness, the arithmetic mean isn’t always the best measure of central tendency. For skewed data or when dealing with outliers, alternative measures may be more appropriate.
Frequently Asked Questions
What is the arithmetic mean used for?
The arithmetic mean is commonly used as a summary statistic to represent the ‘typical’ value in a dataset.
How do you calculate the arithmetic mean?
You can calculate the mean by summing all the values in a dataset and then dividing by the number of values.
Can the arithmetic mean be misleading?
Yes, outliers or skewed data can make the mean less representative of a dataset.
What is the difference between the arithmetic mean and the median?
While both are measures of central tendency, the mean is influenced by all values in a dataset, whereas the median is only affected by the middle value(s).
Is the mean the same as the average?
Yes, in most contexts, the terms are used interchangeably.
How do you calculate a weighted mean?
The weighted mean is calculated by summing the products of each value and its corresponding weight, then dividing by the total sum of weights.
Conclusion
Arithmetic mean is an extraordinarily powerful and versatile tool in the world of statistics. From day-to-day tasks to complex research projects, it plays a pivotal role in simplifying large datasets into understandable figures. While it has its limitations and must be interpreted carefully, it provides an essential foundation upon which much of statistics is built.
Hello, I’m Cansu, a professional dedicated to creating Excel tutorials, specifically catering to the needs of B2B professionals. With a passion for data analysis and a deep understanding of Microsoft Excel, I have built a reputation for providing comprehensive and user-friendly tutorials that empower businesses to harness the full potential of this powerful software.
I have always been fascinated by the intricate world of numbers and the ability of Excel to transform raw data into meaningful insights. Throughout my career, I have honed my data manipulation, visualization, and automation skills, enabling me to streamline complex processes and drive efficiency in various industries.
As a B2B specialist, I recognize the unique challenges that professionals face when managing and analyzing large volumes of data. With this understanding, I create tutorials tailored to businesses’ specific needs, offering practical solutions to enhance productivity, improve decision-making, and optimize workflows.
My tutorials cover various topics, including advanced formulas and functions, data modeling, pivot tables, macros, and data visualization techniques. I strive to explain complex concepts in a clear and accessible manner, ensuring that even those with limited Excel experience can grasp the concepts and apply them effectively in their work.
In addition to my tutorial work, I actively engage with the Excel community through workshops, webinars, and online forums. I believe in the power of knowledge sharing and collaborative learning, and I am committed to helping professionals unlock their full potential by mastering Excel.
With a strong track record of success and a growing community of satisfied learners, I continue to expand my repertoire of Excel tutorials, keeping up with the latest advancements and features in the software. I aim to empower businesses with the skills and tools they need to thrive in today’s data-driven world.
Suppose you are a B2B professional looking to enhance your Excel skills or a business seeking to improve data management practices. In that case, I invite you to join me on this journey of exploration and mastery. Let’s unlock the true potential of Excel together!
https://www.linkedin.com/in/cansuaydinim/