ANOVA and MANOVA: 11 Key Differences
Step into the world of statistics with A Comprehensive Guide to ANOVA and MANOVA: Key Differences and Applications. Discover the 11 crucial differences and learn how to apply these statistical tests for groundbreaking results.
Table of Contents
Introduction
Let’s face it; statistics can be overwhelming. But when you strip away the jargon and convoluted formulas, you’re left with invaluable tools for making sense of our complex world. Welcome to this comprehensive guide on ANOVA and MANOVA—your one-stop resource to understanding the key differences and applications of these statistical tests. If you’re a student, researcher, or data analyst, buckle up because we’re diving deep into these two powerful tools.
A Comprehensive Guide to ANOVA and MANOVA: Key Differences and Applications
ANOVA and MANOVA
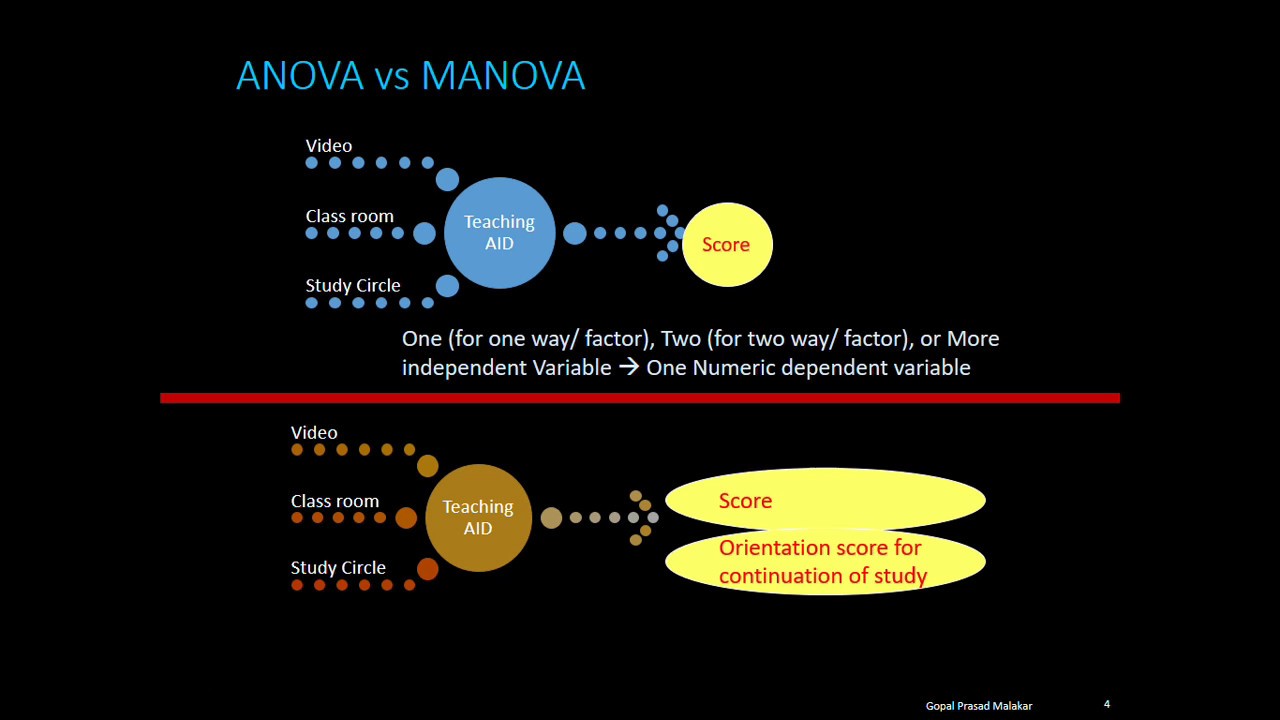
ANOVA (Analysis of Variance) and MANOVA (Multivariate Analysis of Variance) are foundational stones in the field of statistics. While both serve the ultimate aim of hypothesis testing and data interpretation, they differ in several aspects, including their complexity, application areas, and capabilities.
What is ANOVA?
ANOVA, or Analysis of Variance, is a statistical method used to analyze the differences between group means in a sample. In layman’s terms, it helps you figure out if the averages (means) of different groups are genuinely different or if any observed difference is just random noise.
How is ANOVA Used in Various Fields?
The application of ANOVA goes beyond the realm of pure academics. Here’s how:
- Healthcare: For example, medical researchers use it to compare the effectiveness of different treatments.
- Business: It helps in A/B testing to determine which marketing strategy is more effective.
- Psychology: Used to study behavior patterns among different groups.
What is MANOVA?
On the flip side, we have MANOVA or Multivariate Analysis of Variance. Think of it as ANOVA but on steroids. While ANOVA looks at one dependent variable, MANOVA allows for the analysis of multiple dependent variables simultaneously.
Why Use MANOVA?
You might ask, “Why go for MANOVA when ANOVA is simpler?” Here’s why:
- Complexity: When dealing with complex datasets with multiple variables, MANOVA provides more insightful conclusions.
- Interconnected Variables: It helps when the variables under consideration influence each other.
Comparison Table: ANOVA vs. MANOVA
| Aspect | ANOVA | MANOVA |
|---|---|---|
| Dependent Variables | One | Multiple |
| Complexity | Lower | Higher |
| Application Areas | Widespread but simpler scenarios | Complex and interconnected datasets |
11 Key Differences Between ANOVA and MANOVA
Ah, the moment you’ve been waiting for! Here are the 11 key differences:
- Dependent Variables: …
- Mathematical Complexity: …
- Power to Detect Differences: …
- Type I and Type II Errors: …
- Sensitivity: …
- Assumptions: …
- Data Handling: …
- Interactions: …
- Interpretation: …
- Application Areas: …
- Software Requirements: …
Real-world Applications of ANOVA
anova and manova examples
Clinical Trials: A Life-Changing Arena for ANOVA
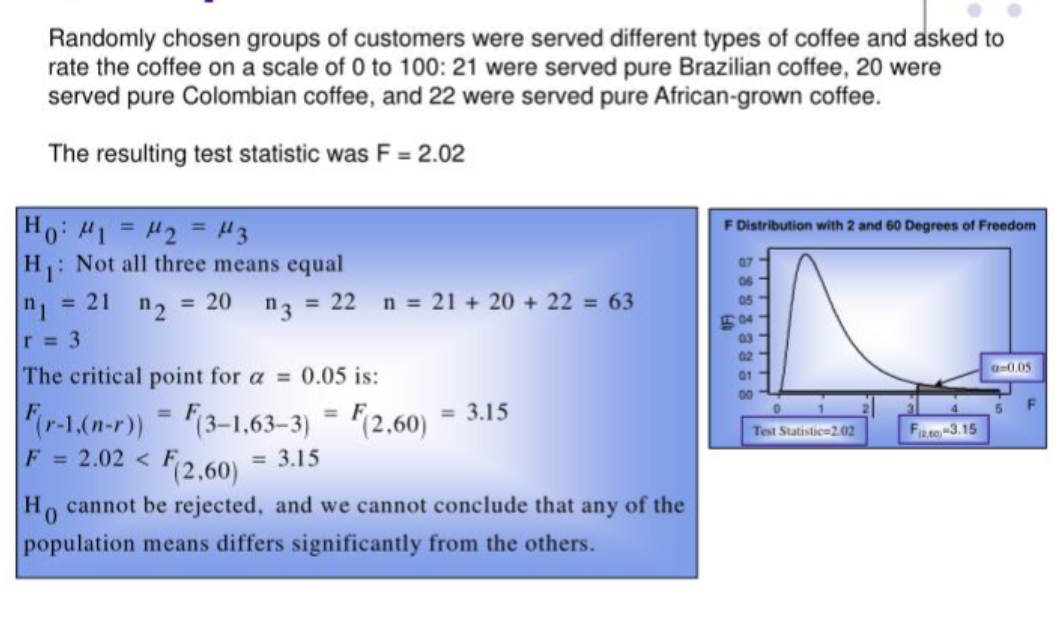
In the world of medical science, particularly in the realm of clinical trials, ANOVA plays an indispensable role. Imagine a scenario where researchers are examining the effectiveness of three different medications for high blood pressure. They could use ANOVA to analyze data from multiple groups of patients—each receiving a different medication—to determine which drug is the most effective. This way, they can scientifically substantiate claims of effectiveness, ensuring that the medication reaching the market is not only efficient but also backed by solid empirical evidence. The outcome of these trials can literally be a matter of life and death, making ANOVA not just a statistical tool but a critical part of healthcare research.
Product Development: Ensuring Quality and Consistency
In the field of manufacturing and product development, maintaining consistent quality is a top priority. Take, for example, a company that produces smartphone batteries. They might run an ANOVA test to compare the lifespan of batteries made in different factories or under different conditions. By analyzing the variance, they can isolate issues, identify the best production methods, and ultimately ensure that the end-users receive a product that meets a certain quality standard. This application of ANOVA directly affects a company’s reputation and market standing, hence its crucial role in product development.
Real-world Applications of MANOVA
Social Sciences: Understanding the Complexity of Human Emotions
MANOVA is especially useful in the field of social sciences where researchers often deal with multiple interconnected psychological variables like stress, anxiety, and depression. By using MANOVA, they can examine how these variables interact with each other across different groups—say, between people who meditate and those who don’t. The ability to analyze multiple dependent variables simultaneously provides a nuanced understanding that’s more aligned with the complexity of human emotions and behavior.
Economics: A New Age Tool for Market Research
In the competitive business landscape, understanding consumer behavior is paramount. MANOVA allows market researchers to analyze multiple consumer-related variables at once, like the influence of age, income, and educational background on product preference. This multipronged insight is invaluable for businesses looking to tailor their products or services to specific demographics, thereby increasing the chances of market success.
How to Perform an ANOVA Test: A Step-by-Step Guide
Define Hypothesis
Start by defining your null hypothesis (H0), which usually states that there is no effect or no difference, and the alternative hypothesis (Ha), which is what you aim to prove.
Collect Data
Gather your data carefully. Make sure it is random, representative, and that your samples are independent of each other.
Choose the Right Software
Software options abound—from Excel and SPSS to Python libraries like SciPy. Choose one based on your comfort level and the complexity of your data.
Input Data
Load your data into the software, making sure it’s structured in a way that the software can understand. Often, this means placing different groups in different columns.
Interpret Results
Post-analysis, focus on the p-value. A low p-value (< 0.05) typically indicates that you can reject the null hypothesis. Examine other outputs like the F-ratio to understand the impact size.
Importance of p-value:
- Rejection of Null Hypothesis: A p-value below the chosen alpha level (commonly 0.05) means that you can reject the null hypothesis. This suggests that your experiment or study found statistically significant results.
- Indicative but Not Conclusive: However, a low p-value is not a measure of the magnitude of an effect. It simply tells you that there is an effect but doesn’t quantify how big or important that effect is.
- Not the Only Measure: Solely relying on the p-value can be misleading. It is possible to have a statistically significant result that is not practically significant.
The F-ratio and Effect Size:
While the p-value tells you whether an effect exists, the F-ratio and measures like Cohen’s d or η² (eta-squared) tell you the magnitude (effect size) of the observed effect.
- F-ratio: It is the ratio of explained variance to the unexplained variance. A large F-ratio suggests that a significant amount of the variance in the dependent variable can be explained by the independent variable(s), which means that your model is a good fit for the data.
- Cohen’s d or η² (eta-squared): These are measures of effect size, indicating how substantial an effect is. Even if a p-value is very low, the actual effect could be trivial if the sample size is large enough.
Things to Keep in Mind:
- Multiple Comparisons: If you are conducting multiple tests, you should consider using corrections like Bonferroni or False Discovery Rate to maintain the overall error rate.
- Context Matters: Always interpret p-values and other statistics like the F-ratio in the context of your research question, the experimental design, and the relevant scientific field.
- Replicability: Even if you find a low p-value and large F-ratio, your results need to be replicable in further studies to be considered valid.
- Data Quality: Ensure that the assumptions for using certain statistical tests are met and that your data is of high quality. Misleading results can occur if these conditions are not met.
In summary, while a low p-value indicates statistical significance, it should not be interpreted in isolation. Other outputs like the F-ratio and effect size measures should also be considered for a comprehensive understanding of the data.
How to Perform a MANOVA Test: A Step-by-Step Guide
Understand Your Variables
Identify all dependent and independent variables you’ll be analyzing. Make sure they are measured on the same scale.
Check Assumptions
Like ANOVA, MANOVA has assumptions—normal distribution, homogeneity of variance-covariance, etc. Ensure your data meets these criteria.
Choose the Software
Again, SPSS, R, and Python libraries are excellent choices. Choose based on your data’s complexity and your comfort level with the software.
Run the Test
Input your data and run the MANOVA test, making sure to select all necessary options for your specific hypotheses and research questions.
Interpret the Results
In addition to the p-value, MANOVA will give you a variety of other statistics like Wilks’ Lambda. Interpret these carefully to draw valid conclusions.
Each of these steps and applications is a critical element in the larger picture of ANOVA and MANOVA utility. Understanding them not only gives you a great toolset for your statistical endeavors but also deepens your appreciation of how these analyses impact various fields significantly.
Frequently Asked Questions
What is the primary aim of using ANOVA or MANOVA?
The main goal is hypothesis testing, to understand if the means of different groups are statistically significantly different.
Why is MANOVA considered more complex than ANOVA?
Because MANOVA deals with multiple dependent variables simultaneously, making it more challenging to interpret.
Can ANOVA and MANOVA be used together?
Yes, they can be complementary, depending on the research question and dataset.
Which software can perform ANOVA and MANOVA tests?
Software like SPSS, R, and Python libraries can perform these tests.
What are Type I and Type II errors in the context of ANOVA and MANOVA?
Type I error occurs when you reject a true null hypothesis, and Type II error occurs when you fail to reject a false null hypothesis.
Are there alternatives to ANOVA and MANOVA?
Yes, alternative methods include t-tests for simpler analyses and mixed models for more complex datasets.
Conclusion
Understanding ANOVA and MANOVA is akin to learning a new language—it opens up a world of possibilities. Whether you’re a data analyst or a researcher, grasping the differences and applications of these two methods will significantly bolster your analytical skills. Now go out there and crunch those numbers!
Hello, I’m Cansu, a professional dedicated to creating Excel tutorials, specifically catering to the needs of B2B professionals. With a passion for data analysis and a deep understanding of Microsoft Excel, I have built a reputation for providing comprehensive and user-friendly tutorials that empower businesses to harness the full potential of this powerful software.
I have always been fascinated by the intricate world of numbers and the ability of Excel to transform raw data into meaningful insights. Throughout my career, I have honed my data manipulation, visualization, and automation skills, enabling me to streamline complex processes and drive efficiency in various industries.
As a B2B specialist, I recognize the unique challenges that professionals face when managing and analyzing large volumes of data. With this understanding, I create tutorials tailored to businesses’ specific needs, offering practical solutions to enhance productivity, improve decision-making, and optimize workflows.
My tutorials cover various topics, including advanced formulas and functions, data modeling, pivot tables, macros, and data visualization techniques. I strive to explain complex concepts in a clear and accessible manner, ensuring that even those with limited Excel experience can grasp the concepts and apply them effectively in their work.
In addition to my tutorial work, I actively engage with the Excel community through workshops, webinars, and online forums. I believe in the power of knowledge sharing and collaborative learning, and I am committed to helping professionals unlock their full potential by mastering Excel.
With a strong track record of success and a growing community of satisfied learners, I continue to expand my repertoire of Excel tutorials, keeping up with the latest advancements and features in the software. I aim to empower businesses with the skills and tools they need to thrive in today’s data-driven world.
Suppose you are a B2B professional looking to enhance your Excel skills or a business seeking to improve data management practices. In that case, I invite you to join me on this journey of exploration and mastery. Let’s unlock the true potential of Excel together!
https://www.linkedin.com/in/cansuaydinim/










