Introduction to one’s complement: Definition, working, and conversions

In the number system, one’s complement is used to represent the negative number in 0 & 1 integers. The one’s complement is the transpose of the binary numbers. Each number system like decimal, hexadecimal, binary, etc. can be converted into one’s complement. In the post, we will learn the definition, working, and conversions of various number systems. And we will also suggest you a one’s complement calculator to ease the process.

What is one’s complement?

According to Wikipedia:

This is a system of numbers in which negative numbers are represented by the transpose of the binary number representation of their equivalent positive numbers.

In this number system, a number can be converted from positive to negative or negative to positive by calculating its one’s complement. This is, all the zero values of binary numbers should be converted into one and all the ones into zeros.

Working of one’s complement

Follow the below steps to convert any number system.

First of all, convert the number systems into decimal or base 10 number systems.

• Then convert the decimal number into a binary number system or base 2 number system.
• After getting the result of a binary number, invert zeros into ones and ones into zeros.
• In the case of a negative decimal number, convert the number into a binary number according to the positive number then invert the symbols to take the binary number of a decimal number.
• Then take the transpose of the negative binary number.

You can convert ASCII, hexadecimal numbers, decimal numbers, and binary numbers into one’s complement by following the above-mentioned steps.

How to convert binary, decimal, and hex numbers?

Let us discuss how to convert the decimal, binary, and hexadecimal numbers briefly.

Binary to one’s complement

A binary number system is a base two number system in which 0 & 1 numerals are involved. Binary numbers can be represented in one’s complement. You have to follow the below steps to convert the binary number into one’s complement.

• Take the binary number.
• Invert the numerals of the binary numbers.
• The inverted value will be one’s complement of the binary number.

Example

Convert 11100101 into one’s complement.

Solution

Step 1: Take the given base two number.

11100101

Step 2: Now invert the numerals of the base 2 number.

1 1 1 0 0 1 0 1

0 0 0 1 1 0 1 0

Hence, 00011010 is the one’s complement of the given base 2 number.

Decimal to one’s complement

The decimal number system is a base 10 number system in which 0 to 9 numerals are involved. The decimal number system can be represented as one’s complement. Follow the below steps to convert a decimal number into one’s complement.

• Take the positive or negative base 10 number.
• Convert the decimal number into a binary number.
• Invert the numerals of the binary numbers.
• The inverted value will be one’s complement of the positive binary number.
• In the case of a negative base 10 number, convert it into the binary number according to the positive decimal number then invert the numerals to take the binary number of a decimal number.
• Then take the transpose of the negative binary number.
• The result will be the one’s complement of the base 10 number system.

Example 1: For a positive base 10 number

Convert 123 into one’s complement.

Solution

Step 1: First of all, convert the given base 10 number into base 2 number system.

2	123
2	61 – 1
2	30 – 1
2	15 – 0
2	7 – 1
2	3 – 1
	1 – 1

 

Hence, 1111011 is a base 2 number of 123.

Step 2: Now invert the numerals of the binary number to get the one’s complement.

1 1 1 1 0 1 1

0 0 0 0 1 0 0

Hence, 0000100 is one’s complement of 123.

You can also use a one’s complement calculator to convert the number systems into one’s complement. Follow the below steps to use this tool.

Step-1: Select the number system.

Step 2: Select the bits.

Step-3: Input the given number.

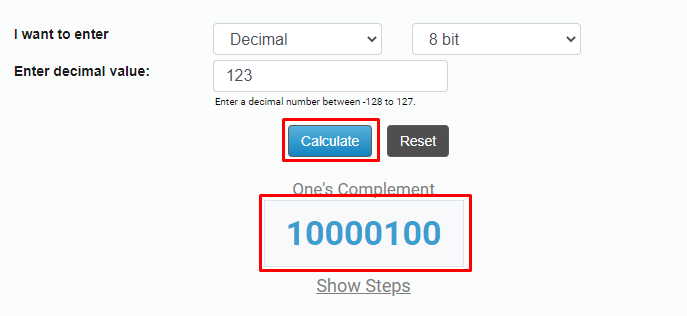
Step 4: Hit the calculate button to get the result from one’s complement calculator.

Step 5: Press the show more button to view the solution with steps.

Example 2: For a negative base 10 number

Convert -133 into one’s complement.

Solution

Step 1: First of all, convert the given corresponding positive decimal number into base 2 number system.

2	133
2	66 – 1
2	33 – 0
2	16 – 1
2	8 – 0
2	4 – 0
2	2 – 0
	1 – 0

 

Hence, 10000101 is a base 2 number of 133.

Step 2: Now invert the numerals of the binary number to get the binary number of -133.

1 0 0 0 0 1 0 1

0 1 1 1 1 0 1 0

Hence, 01111010 is binary number of -133.

Step 3: Take the transpose of a negative binary number.

0 1 1 1 1 0 1 0

1 0 0 0 0 1 0 1

Hence, 10000101 is one’s complement of -133.

Hexadecimal to one’s complement

The hexadecimal number system is a base 16 number system in which 0 to 15 numerals are involved. The base 16 number can be represented in one’s complement. Follow the below steps to convert hex to one’s complement.

• Convert the given base 16 number into a decimal number system.
• Convert the base 10 number into a binary number.
• Invert the numerals of the base 2 number.
• The inverted value will be one’s complement of the binary number.

Example

Convert 125 into one’s complement.

Solution

Step 1: First of all, convert the given base 16 number into a decimal number.

293 is the decimal number of 125.

Step 2: Convert 293 into binary number.

2	293
2	146 – 1
2	73 – 0
2	36 – 1
2	18 – 0
2	9 – 0
2	4 – 1
2	2 – 0
	1 – 0

Hence, 100100101 is a binary number of 293.

Step 3: Now invert the numerals of the base 2 number.

1 0 0 1 0 0 1 0 1

0 1 1 0 1 1 0 1 0

Hence, 011011010 is one’s complement of the given base 16 number.

Summary

Now you are witnessed that the conversion of any number system into one’s complement is not difficult. You can easily convert the base 2, base 10, and base 16 number system just by learning the above post and using a one’s complement calculator too.

Tags: number systems one's complement one's complement calculator one's complement to decimal two's complement vs one's complement